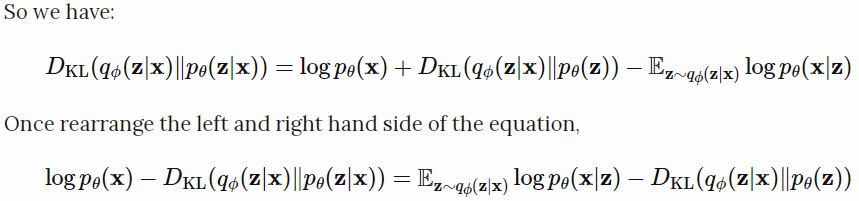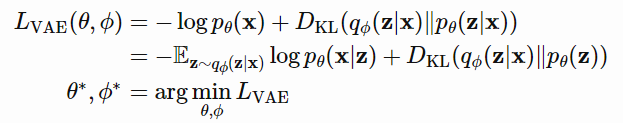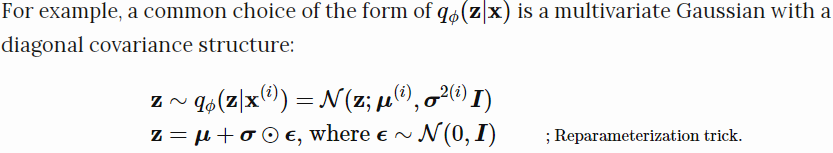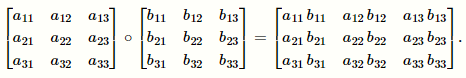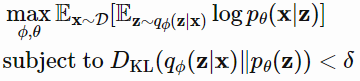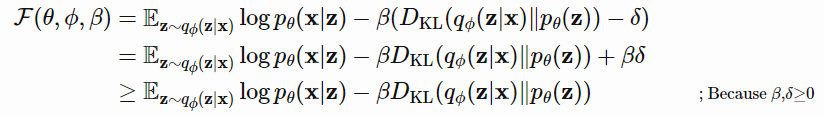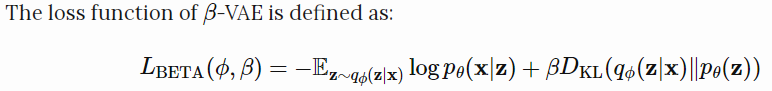Autoencoder
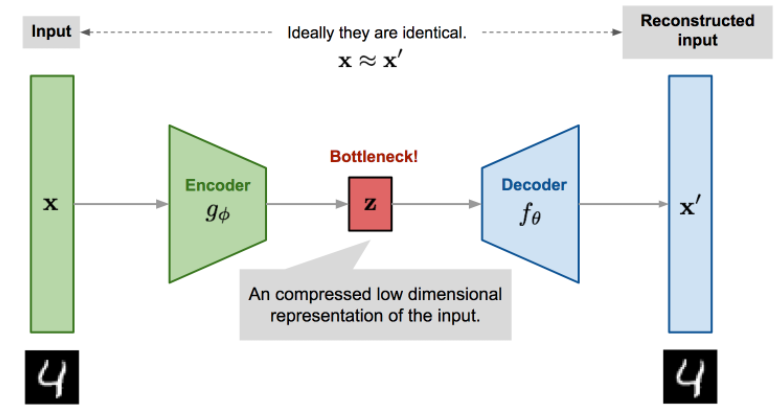
自编码器是一种神经网络,其设计目的是在压缩数据的同时,以无监督的方式学习恒等函数来重构原始输入,从而发现一种更有效的压缩表示。
- Encoder network $g_\phi(.)$:把原始的高维输入转换成潜在的低维编码,输入大小大于输出大小。
- Decoder network $f_\theta(.)$:从编码中复原数据.
- bottleneck layer 是 $z=g_\phi(x)$
花书以 $h=f(x)$ 表示编码器的输出
- 重建数据 :$x'=f_\theta(g_\phi(x))$
维度压缩就像PCA或MF,而从编码再重建数据,好的中间表示不仅可以捕获潜在变量,也有利于整个的解压缩过程,属于是对自编码器进行了显式优化。
参数$(\theta,\phi)$一起学习,令$x\approx f_\theta(g_\phi(x))$,有很多方法可以量化这两个向量之间的差异,比如激活函数为sigmoid时的交叉熵,或者简单的MSE损失
$$L_{AE}(θ,ϕ)=\frac{1}{n}∑_{i=1}^{n}(x^{(i)}−f_θ(g_ϕ(x^{(i)})))^2$$
在花书中,缩写为 $L(x,g(f(x)))$
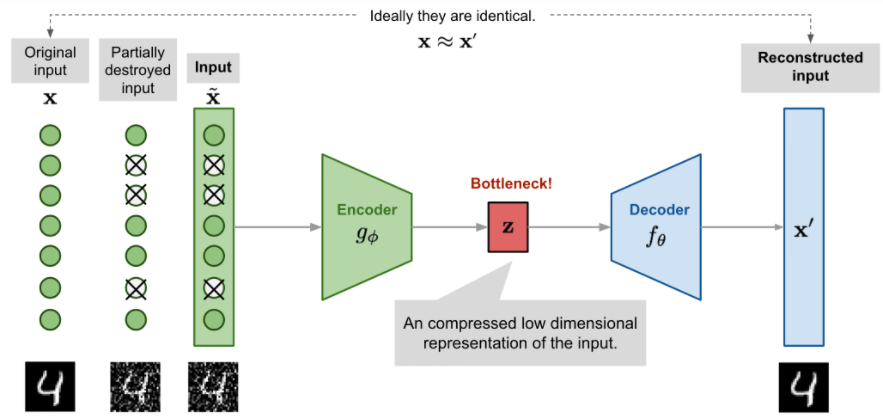
Denoising Autoencoder (DAE)
当网络参数大于数据点数的时候,面临着过拟合的风险,为避免过拟合和提高鲁棒性,输入被随机方式加入噪声或掩盖输入向量的某些值而部分损坏,记为
$$\tilde{x}^{(i)} \sim \mathcal{M_D}(\tilde{x}^{(i)}|x^{(i)})$$
$\mathcal{M_D}$定义了从真实的数据样本到噪声或损坏的数据样本的映射
最小化 $L(x,g(f(\tilde{x})))$,重建的数据是无噪声的
Sparse Autoencoder
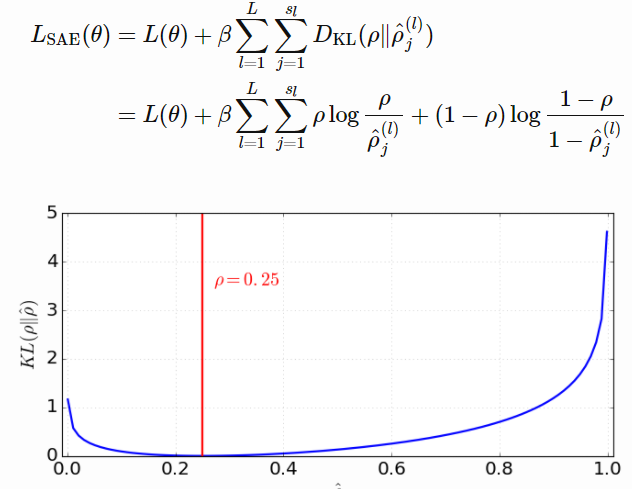
迫使模型在同一时间只有少量的隐藏单元被激活,一个隐藏层的神经元应该在大部分时间被灭活。 一隐藏层神经元被激活的比例是一个参数 $\hat{\rho}$ ,期望应该是一个很小的数 $\rho$ (叫做稀疏参数),通常 $\rho=0.05$
这个约束是通过在损失函数中添加一个惩罚项实现的,KL散度测量了平均值为$\rho$和$\hat{\rho}$两个伯努利分布(Bernoulli distributions)之间的差别。用超参数$\beta$来控制对稀疏损失的惩罚程度。
Notation: 关于自编码器符号,花书和From Autoencoder to Beta-VAE是有区别的,具体是Encoder、Decoder(相反)和中间数据表示符号(z 、h)不同.
Structured probabilistic model
结构化概率模型使用图来描述概率分布中随机变量之间的直接相互作用,从而描述一个概率分布,这些模型也通常被称为图模型(graphical model) 。
忽略间接相互作用,能大大减少模型的参数个数,更小的模型大大减少了在模型存储、模型推断以及在模型中采样时的计算开销。
图描述模型结构
有向模型
有向图模型(directed graphical model),也被称为信念网络(belief network)或者贝叶斯网络(Bayesian network)。
变量$x$的有向概率模型是通过有向无环图$\mathcal{G}$和一系列局部条件概率分布来定义的。其中,$P_{a\mathcal{G}}(x_i)$表示节点$x_i$的所有父节点。 $$p(x)=\prod_ip(x_i|P_{a\mathcal{G}}(x_i))$$
无向模型
无向模型(undirected model),也被称为马尔可夫随机场(Markov random field,MRF)或者马尔可夫网络。
并不是所有情况的相互作用都有一个明确的方向关系,当相互作用没有本质性的指向或者是明确的双向关系作用时,用无向模型更合适。
对于图中的每一个团 $\mathcal{C}$ (图中的团是图中节点的一个子集,其中的点是全连接的), 一个因子 $\phi(\mathcal{C})$ (也被称为团势能(clique potential)),衡量了团中每个变量每一种可能的联合状态所对应的密切程度。它们一起定义了未归一化概率函数: $$\tilde{p}(x)=\prod_{\mathcal{C\in G}}\phi(\mathcal{C})$$
配分函数
为了保证概率之和或积分为1,需要使用对应的归一化的概率分布
$$p(x)=\frac{1}{Z}\tilde{p}(x)$$
$$Z = \int \tilde{p}(x) dx$$
当函数$\phi$固定时,$Z$就是个常数,如果函数$\phi$带有参数,$Z$就是这些参数的一个函数,$Z$被称为配分函数。
分离与d-分离
想知道在给定其他变量子集的值时,哪些变量子集彼此条件独立。
无向模型中,识别图中的条件独立性是非常简单的,这时候图中隐含的条件独立性称为分离。 如果变量a和b的连接路径仅涉及未观察变量,那么这些变量不是分离的。如果之间没有路径,或者所有路径都包含可观测的变量,那么他们是分离的。认为仅涉及未观察到的变量的路径是“活跃”的,包括可观察变量的路径称为“非活跃”的。
有向模型中,这些概念叫做d-分离。
VAE: Variational Autoencoder
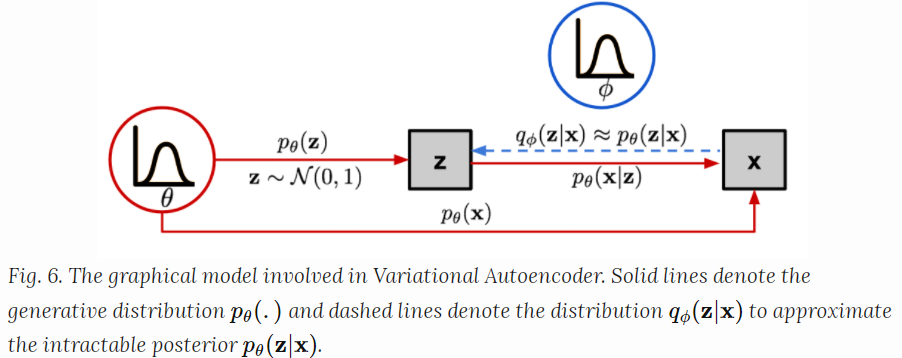
不想把输入映射到一个固定的向量,而是要把它映射到一个概率分布$p_\theta$ 。输入$x$和latent encoding vector $z$ 之间的关系可以被下面的定义:
- 先验分布 $p_\theta(z)$
- 似然分布 $p_\theta(x|z)$
- 后验分布 $p_\theta(z|x)$
为了生成一个像是真实数据的样本$x^i$,以下步骤:
- 从先验分布$p_{\theta^*}(z)$中抽样$z^i$
- 从条件概率分布$p_{\theta^*}(x|z=z^i)$中生成值$x^i$
最佳参数 $\theta^*$ 是使生成真实样本数据概率最大的参数。
$$ \theta^* = arg \ max_\theta\prod^n_{i=1}p_\theta(x^i)$$
通常会变形为log形式,将乘法换成加法
$$\theta^* = arg \ max_\theta\prod^n_{i=1}log \ p_\theta(x^i)$$
$$p_\theta(x^i)=\int p_\theta(x^i|z)p_\theta(z)dz$$
但是检查所有可能的$z$值,并将对应的x的概率积分的代价是很昂贵的。引入概率分布$q_\phi(z|x)$去近似$p_\theta(z|x)$,用输出$x$给定输入可能的$z$
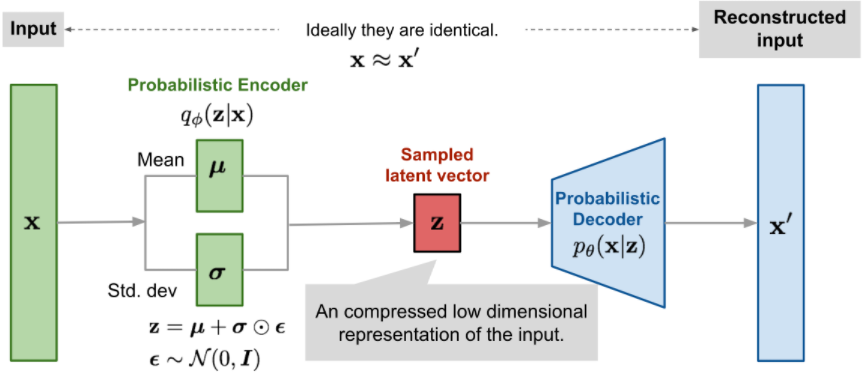
如上,现在的结构很像一个自编码器
- $p_\theta(x|z)$ 定义了一个生成模型,类似于解码器,$p_\theta(x|z)$ 也叫概率解码器
- 估计的函数 $q_\phi(z|x)$ 是概率编码器
Loss function:ELBO
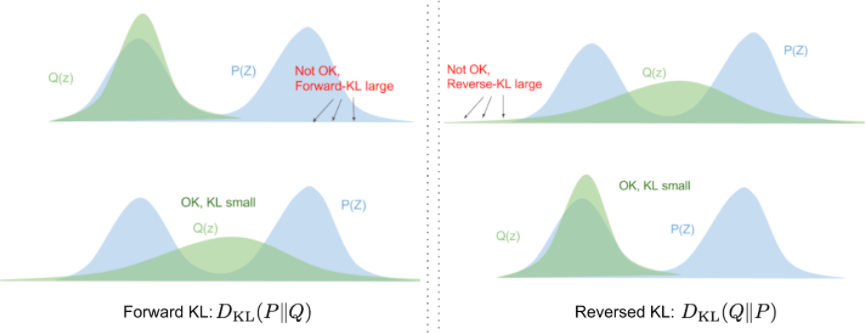
可以用KL散度去量化这两个分布之间的距离,$D_{KL}(X||Y)$ ,度量用分布Y表示X时丢失了多少信息。
我们想要参数$\phi$,使得$D_{KL}(q_\phi(z|x)||p_\theta(z|x))$最小
[Bayesian Variational methods -- Eric Jang](https://blog.evjang.com/2016/08/variational-bayes.html)
这个是学习真实分布时想要最大化的:最大化log形式的产生真实数据的可能性( $log \ p_\theta(x)$ ),最小化真实后验分布和估计的后验分布的差异。
损失函数的定义如下:
在变分贝叶斯方法中,这个损失函数被称为变分下界或证据下界。KL散度总是非负的,$-L_{VAE}$ 就是 $log \ p_\theta(x)$ 的下界。
$$-L_{VAE}=log \ p_\theta(x) - D_{KL}(q_\phi(z|x)||p_\theta(z|x)) \leq log \ p_\theta(x)$$
最小化损失函数,就能最大化产生真实数据样本的概率下界
Reparameterization Trick (重新参数化技巧)
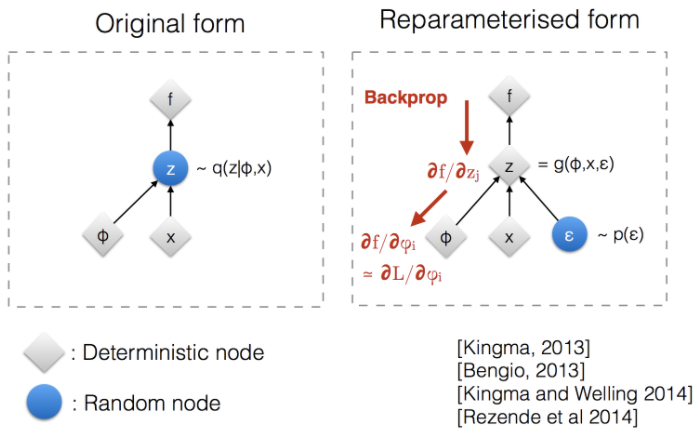
损失函数中调用了$z\sim q_\theta(z|x)$的生成样本,采样是一个随机过程,不能反向传播梯度,为了使之可以训练,引入了重新参数化技巧。 通常是将随机变量$z$转化为确定性变量 $z=\mathcal{T}_\theta(x,\epsilon)$,其中$\epsilon$是一个独立的随机变量。
上图说明了重新参数化技巧如何使$z$采样过程可训练
Hadamard 积,只在两个相同维度的矩阵(A\B)中定义,记作 $A\odot B \ or \ A \circ B$
运算则是逐元素相乘
$\beta$-VAE
如果 inferred latent representation $z$ 只对单一生成因素敏感,对其他因素不敏感,叫这种表示为解纠缠(disentangled)或因子化的(factorized)。好处是可解释性好,而且易于迁移到其他任务。
例如,一个模型在训练人脸照片时可能会捕捉肤色、头发颜色、头发长度、情绪、是否戴眼镜以及许多其他相对独立的因素。这样的解纠缠表示对于人脸图像的生成是非常有益的。
$\beta$-VAE是修改的VAE,特别强调发现解纠缠的潜在因素。
KKT条件下可以重写为有拉格朗日乘子$\beta$的拉格朗日函数,上述只有一个不等式约束的优化问题等价于最大化方程$\mathcal{F}(\theta,\phi,\beta)$
$\beta$作为超参数,如果$\beta=1$,和VAE相同,更高的$\beta$值强化了对latent bottleneck的约束,能增强解纠缠。(和正则化中的权重衰减类似)
参考
- 花书第十四章
- 花书 第16章 深度学习中的结构化概率模型
- From Autoencoder to Beta-VAE
- Variational autoencoders.